Search a 2D Matrix
PROBLEM
You are given an m x n integer matrix matrix with the following two properties:
Each row is sorted in non-decreasing order.
The first integer of each row is greater than the last integer of the previous row.
Given an integer target, return true if target is in matrix or false otherwise.
You must write a solution in O(log(m * n)) time complexity.
Example1
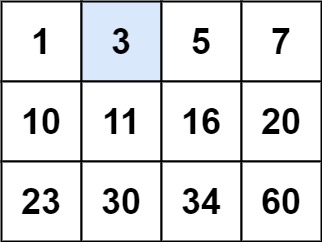
*Input*: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
*Output*: true
Example2

*Input*: matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
*Output*: false
SOLVING
we’ll use Binary Search exact value to solve this problem
Steps
- Find the row:
- If
firstelement of the row is superior of thetargetreturn false - If
lastelement of the row i inferior of thetargetgo tonextrow - Otherwise it’s the good
rowto search
- If
- Search in the row,
binary searchexact valueLeftPtrto first element andRightPtrto last element- Take the middle between left and right ptr:
- If equal to target
return true - If superior
LeftPtrequal middleIndex+1 - Else inferior
RightPtrequal middleIndex-1
- If equal to target
- Return
falsebecause that mean target not found
Code
class Solution {
public:
bool searchMatrix(vector<vector<int>> &matrix, int target) {
int rowSize = matrix[0].size();
int leftPtr = 0, rightPtr = rowSize - 1;
for (int i = 0; i < matrix.size(); i++) {
auto row = matrix[i];
if (row[rightPtr] < target) continue;
if (row[leftPtr] > target) return false;
while (leftPtr <= rightPtr) {
int m = (leftPtr + rightPtr) / 2;
if (row[m] == target)
return true;
else if (row[m] < target)
leftPtr = m + 1;
else
rightPtr = m - 1;
}
}
return false;
}
};