Rotting Oranges
PROBLEM
You are given a m x n grid where each cell can have one of three values:
0representing an empty cell,1representing a fresh orange, or2representing a rotten orange.
Every minute, any fresh orange that is 4-directionally adjacent to a rotten orange becomes rotten.
Return the minimum number of minutes that must elapse until no cell has a fresh orange. If this is impossible, return -1.
Example1
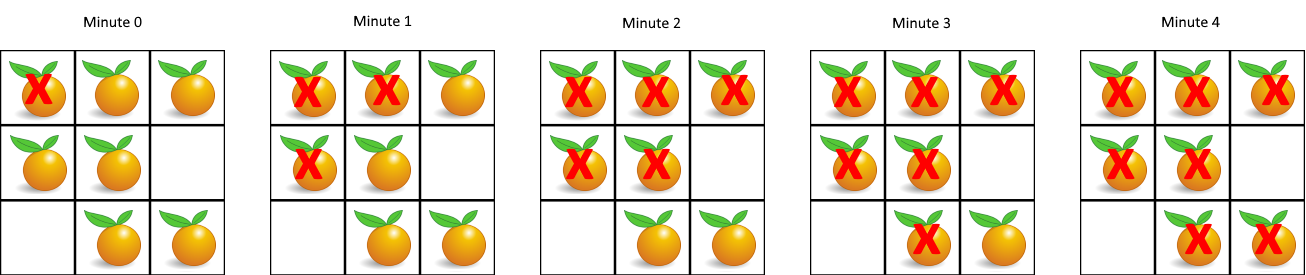
=Input=: grid = [[2,1,1],[1,1,0],[0,1,1]]
=Output=: 4
Example2
=Input=: grid = [[2,1,1],[0,1,1],[1,0,1]]
=Output=: -1
Explanation: The orange in the bottom left corner (row 2, column 0) is never rotten, because rotting only happens 4-directionally.
Example3
=Input=: grid = [ [0,2] ]
=Output=: 0
Explanation: Since there are already no fresh oranges at minute 0, the answer is just 0.
SOLVING
We’ll use Breadth-first Search method
Steps
- Create a queue and another matrix called
turn - Browse the matrix to push in a queue the position of the
rotten orangesand inturnthe value0.- While queue isn’t empty:
- Pop the queue to get position from last
rotten oranges - Get the neighboors of this orange:
- if it’s an
fresh orangeadd it to the queue and change it’s value torotten - In
turnput the value of turn of thisparent + 1
- if it’s an
- Create a variable
turnMax - Browse the matrix:
- if there is a
fresh orangereturn -1 - If it’s a
rotten orangecheck if it’s turn is bigger thanturnMaxif yes update it
- if there is a
- Return
turnMax
Code
class Solution {
public:
int orangesRotting(vector<vector<int>> &grid) {
m = grid.size();
n = grid[0].size();
auto turn = vector(m, vector<int>(n, -1));
queue<pair<int, int>> q;
// Step 1 push into queue all rotten oranges
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
if (grid[r][c] == 2) {
turn[r][c] = 0;
q.push({r, c});
}
}
}
// Step 2 make every turn by rotting oranges next to your rotten oranges
while (!q.empty()) {
pair<int, int> current = q.front();
q.pop();
for (int indexNeighboor = 0; indexNeighboor < 4; indexNeighboor++) {
int newR = current.first + neighboorR[indexNeighboor];
int newC = current.second + neighboorC[indexNeighboor];
if (newR < 0 || newR >= m || newC < 0 || newC >= n ||
grid[newR][newC] != 1)
continue;
turn[newR][newC] = turn[current.first][current.second] + 1;
grid[newR][newC] = 2;
q.push({newR, newC});
}
}
// Step 3 find a fresh orange or update your max turn value
int answer = 0;
for (int r = 0; r < m; r++) {
for (int c = 0; c < n; c++) {
if (grid[r][c] == 1)
return -1;
else if (grid[r][c] == 2)
answer = max(answer, turn[r][c]);
}
}
return answer;
}
private:
int m;
int n;
const int neighboorR[4] = {0, 0, -1, +1};
const int neighboorC[4] = {-1, +1, 0, 0};